Volume Of Pyramid Square Base

Volume of a Correct Square Pyramid

The volume of a correct square pyramid is the space occupied by the right square pyramid. A correct square pyramid is a three-dimensional geometric shape that has a right square base and 4 triangular faces that are joined at a vertex. Allow's acquire how to find the volume of a right square pyramid with the aid of a few solved examples and practice questions.

1.	What is Volume of a Correct Square Pyramid?
2.	Formula of Volume of a Right Square Pyramid
3.	How to Find the Volume of a Right Square Pyramid?
4.	FAQs on Right Square Pyramid Volume

What is Book of a Right Square Pyramid?

The volume of a right foursquare pyramid is the number of unit cubes that tin can fit into it. A correct square pyramid is a three-dimensional shape that has a right foursquare base of operations and four triangular faces that are joined at a vertex. A correct square pyramid is a polyhedron (pentahedron) with five faces. The unit of measurement of volume is "cubic units". For example, it tin be expressed equally chiliad³, cm³, in³, etc depending upon the given units.

Parts of a right square pyramid

A right square pyramid has three components.

The summit point of the pyramid is called the apex.
The bottom right square is called the base.
The triangular sides are chosen faces.

Formula of Book of a Right Foursquare Pyramid

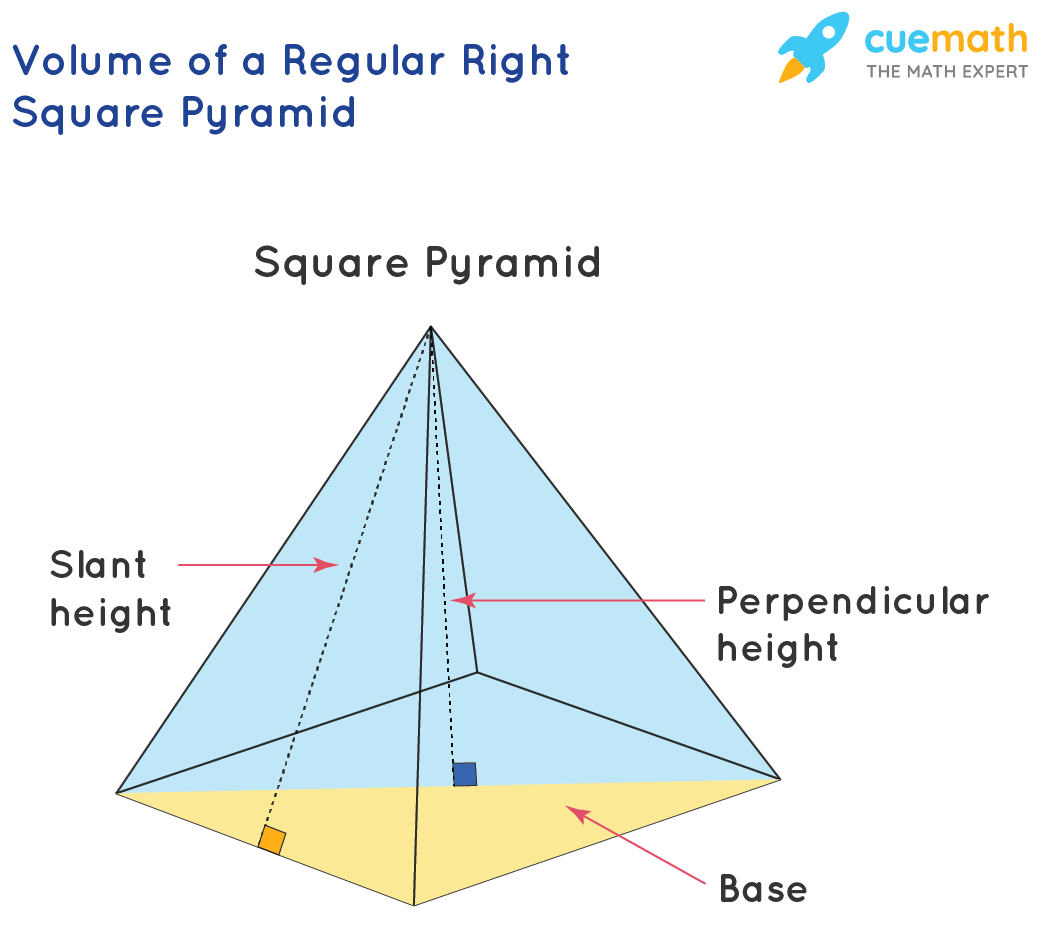
Volume of a right square pyramid formula

The formula to make up one's mind the volume of a right square pyramid is Five = one/three × bⁱⁱ × h where "b" is the length of the base of operations and "h" is the perpendicular meridian. The relation between slant meridian, perpendicular acme, and the base is given past using Pythagoras Theorem s^two = h² + (b/2)² where "s", "h" and "b" are slant height, the top of perpendicular, and base length of the right square pyramid, respectively. Thus, the volume of the right foursquare pyramid is given by replacing the given dimensions in the formula Five = one/3 × b² × h.

How to Find the Book of a Correct Square Pyramid?

As we learned in the previous section, the book of a right square pyramid could be found using \(\dfrac{1}{3} \times \text{b}^two \times \text{h}\). Thus, we follow the below steps to discover the volume of a right square pyramid.

Step 1: Determine the base expanse (b²) and the top (h) of the pyramid.
Step 2: Find the volume using the formula 1/3 × bⁱⁱ × h
Step 3: Represent the final answer with cubic units.

Instance: Discover the volume of the right square pyramid having height and length of the base edge of ix units and 5 units respectively.

Solution: Given that h = 9 units and b = v units.

And so, the volume of the right foursquare pyramid is Five = 1/three × b² × h
⇒ 5 = i/3 × 5² × nine
⇒ V = 5ⁱⁱ × 3 = 75 cubic units

Answer: The volume of the right square pyramid is 75 cubic units.

Solved Examples on Book of a Right Square Pyramid

Case 1: Julia has a vessel in the grade of an inverted regular right foursquare pyramid that has to be filled with water. The altitude of the vessel is 10 inches and the length of the base edge is 7 inches. What is the book of water Julia can fill in the vessel?

Solution: Given h = 10 inches and b = vii inches

The volume of the vessel is given by V = 1/iii × b² × h
⇒ V = ane/3 × vii² × x
⇒ V = 490/3
⇒ V = 163.33 cubic inches

Respond: Thus, the volume of the vessel is 163.33 in³.
Example ii: What will be the volume of a regular square pyramid with base of operations sides 10 cm and a tiptop of eighteen cm?

Solution: Given that b = x cm and h = 18 cm

The formula for the volume of a square pyramid is given by 5 = one/3 × b² × h

The area of the base = The square of base of operations length = xⁱⁱ or 100 cm².
Putting the values bⁱⁱ = 100 and h = 18 in the formula.

V = 1/3 × 100 × xviii = 600 cm^three.

Answer: The volume of the right square pyramid is 600 cm^three.

go to slidego to slide

Breakdown tough concepts through simple visuals.

Math will no longer be a tough subject, especially when you empathise the concepts through visualizations.

Book a Free Trial Class

Practice Questions on Book of a Correct Square Pyramid

go to slidego to slide

FAQs on Volume of a Right Square Pyramid

What is the Volume of a Right Square Pyramid?

The volume of a right square pyramid is defined as the number of unit cubes that tin can fit into a correct foursquare pyramid. A right square pyramid is a three-dimensional geometric shape that has a correct foursquare base and four triangular faces that are joined at a vertex.

What Units Are Used With the Volume of the Right Foursquare Pyramid?

The unit of measurement used with the volume of the right square pyramid is given in cubic units. For example, thousand^three, cm³, in³, etc depending upon the given units.

What is the Formula of the Book of the Correct Square Pyramid?

The formula of the volume of the right square pyramid is given as Five = 1/iii × Base Expanse × Top = 1/3 × b² × h where bⁱⁱ shows the base area and h shows the elevation of the right foursquare pyramid.

How to Find the Volume of a Correct Square Pyramid?

The book (V) of a correct square pyramid can be plant past using the following steps:

Step 1: Discover the base of operations area (b²) and the height (h) of the pyramid.
Step two: Determine the volume using the formula 1/3 × b² × h
Pace 3: Now, write the final answer with cubic units.

How to Find the Volume of a Right Foursquare Pyramid with Camber Height?

The volume (V) of a right square pyramid tin exist constitute by using the following steps:

Step 1: Identify the given dimensions of the right square pyramid.
Step 2: Find the missing dimension using the formula s² = h^two + (b/2)² where "s", "h", and "b" are slant height, the pinnacle of perpendicular, and base length of the right square pyramid, respectively.
Step 2: Make up one's mind the volume using the formula V = 1/3 × bⁱⁱ × h
Step 3: At present, write the final reply with cubic units.

What Happens to the Volume of a Right Square Pyramid If the Height of the Pyramid is Doubled?

The volume of the right square pyramid is doubled if the acme of the pyramid is doubled as "h". In the formula, 5 = 1/3 × b² × h, substitute pinnacle = 2h, V = 1/3 × b² × (2h) = two × (1/iii × b² × h) which gives double the volume of the original book of the correct square pyramid.

What Happens to the Book of a Right Square Pyramid If the Base of operations of the Pyramid is Halved?

The volume of the right square pyramid becomes one-4th the original volume if the base of the pyramid is halved as "b/2". In the formula, V = one/3 × b² × h, substitute base edge = b/2, V = i/3 × (b/2)² × h = (1/four) × (i/3 × b² × h) which gives one fourth the volume of the original volume of the correct square pyramid.