Is A Kite A Quadrilateral

Proving that a quadrilateral is a kite is a like shooting fish in a barrel. Ordinarily, all you have to do is use congruent triangles or isosceles triangles. Here are the ii methods:

• If two disjoint pairs of consecutive sides of a quadrilateral are congruent, then it's a kite (reverse of the kite definition).

• If one of the diagonals of a quadrilateral is the perpendicular bisector of the other, and so it's a kite (converse of a property).

When you lot're trying to evidence that a quadrilateral is a kite, the following tips may come in handy:

• Check the diagram for congruent triangles. Don't fail to spot triangles that look congruent and to consider how CPCTC (Corresponding Parts of Congruent Triangles are Congruent) might assistance yous.

• Keep the first equidistance theorem in heed (which you might employ in addition to or instead of proving triangles congruent): If two points are each (one at a time) equidistant from the endpoints of a segment, and so those points make up one's mind the perpendicular bisector of the segment. (Here'south an easy style to think about it: If you accept two pairs of congruent segments, so at that place's a perpendicular bisector.)

• Depict in diagonals. One of the methods for proving that a quadrilateral is a kite involves diagonals, so if the diagram lacks either of the kite'southward ii diagonals, try drawing in one or both of them.

At present become prepare for a proof:

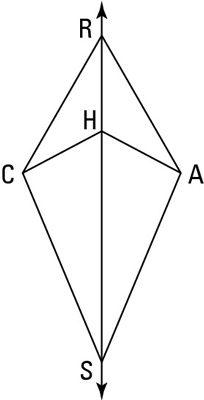
Game plan: Here's how your plan of attack might work for this proof.

• Annotation that ane of the kite's diagonals is missing. Describe in the missing diagonal, segment CA.

• Check the diagram for congruent triangles. Afterward cartoon in segment CA, there are half-dozen pairs of congruent triangles. The two triangles most likely to aid you are triangles CRH and ARH.

• Prove the triangles coinciding. You can use ASA (the Bending-Side-Angle theorem).

• Use the equidistance theorem.

  

  And then, using the equidistance theorem, those two pairs of congruent sides determine the perpendicular bisector of the diagonal y'all drew in. Over and out.

Check out the formal proof:

Statement 1 :

Reason for statement ane : Ii points determine a line.

Argument 2 :

Reason for statement 2 : Given.

Argument 3 :

Reason for statement three : Definition of bisect.

Statement 4 :

Reason for statement iv : Reflexive Belongings.

Statement 5 :

Reason for statement 5 : Given.

Statement vi :

Reason for statement 6 : Definition of bifurcate.

Argument 7 :

Reason for statement 7 : If ii angles are supplementary to two other congruent angles (angle CHS and angle AHS), so they're congruent.

Statement eight :

Reason for statement viii : ASA (3, iv, 7).

Statement 9 :

Reason for argument nine : CPCTC.

Statement 10 :

Reason for statement 10 : CPCTC.

Statement 11 :

Reason for statement 11 : If two points (R and H) are each equidistant from the endpoints of a segment (segment CA), so they determine the perpendicular bisector of that segment.

Argument 12 :

Reason for statement 12 : If 1 of the diagonals of a quadrilateral (segment RS) is the perpendicular bisector of the other (segment CA), and then the quadrilateral is a kite.

About This Article

This article can be plant in the category:

• Geometry ,

Is A Kite A Quadrilateral,

Source: https://www.dummies.com/article/academics-the-arts/math/geometry/how-to-prove-that-a-quadrilateral-is-a-kite-188056/

Posted by: bellprelf1959.blogspot.com

Share this post